| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Exercise 10.1 | Example 1 to 3 (Before Exercise 10.2) | Exercise 10.2 |
Chapter 10 Circles
Welcome to the solutions guide for Chapter 10: Circles. While circles were explored in Class 9 covering chords, arcs, and angles, this chapter delves into a specific and crucial aspect of circle geometry: the interaction between lines and circles, particularly focusing on the properties of tangents. A tangent represents a line that just 'touches' a circle without cutting through its interior, a concept fundamental in geometry and calculus (where it relates to instantaneous rates of change). Understanding tangents and their associated theorems allows us to solve a unique set of geometric problems involving distances, angles, and properties of figures related to circles.
The solutions begin by clearly distinguishing between a secant (a line that intersects a circle at two distinct points) and a tangent. A tangent is formally defined as a line that intersects the circle at precisely one point. This unique intersection point is known as the point of contact. Visualizing this 'touching' property is key to grasping the subsequent theorems. It's also established that from any single point on the circle, only one tangent can be drawn.
Two foundational theorems govern the behavior of tangents, forming the backbone of this chapter's problem-solving techniques:
Theorem 10.1 states a critical perpendicular relationship: The tangent at any point of a circle is perpendicular ($\perp$) to the radius through the point of contact. This means the angle formed between the tangent line and the radius drawn to the point where the tangent touches the circle is always $90^\circ$. The solutions often detail the proof of this theorem, typically by demonstrating that the radius represents the shortest possible distance from the center to any point on the tangent line, hence it must be perpendicular. Applications explored in the solutions include calculating angles in figures involving tangents, radii, and chords connected to the point of contact, often utilizing the right angle formed.
Theorem 10.2 addresses tangents drawn from a single point outside the circle. It states that the lengths of tangents drawn from an external point to a circle are equal. If a point P lies outside a circle, and tangents from P touch the circle at points A and B, then the length $PA$ is equal to the length $PB$. The solutions typically provide the proof using RHS (Right angle-Hypotenuse-Side) congruence, achieved by joining the center to the external point and the points of contact, forming two congruent right-angled triangles. This theorem has numerous powerful applications demonstrated in the solutions, such as:
- Calculating unknown lengths of tangent segments.
- Proving important properties related to quadrilaterals that circumscribe a circle (i.e., all four sides are tangent to the circle). For example, proving that opposite sides of such a quadrilateral subtend supplementary angles at the center of the circle, or proving that if a parallelogram circumscribes a circle, it must necessarily be a rhombus.
- Solving complex geometric problems where tangents from multiple external points are involved.
Beyond these core theorems, the solutions also reinforce understanding the number of tangents possible from a point relative to the circle's position: zero tangents can be drawn from a point lying inside the circle, exactly one tangent from a point on the circle, and exactly two tangents from an external point. Exercises frequently require a synthesis of knowledge, demanding that students combine these tangent theorems with previously learned concepts like the Pythagoras theorem, properties of triangles (isosceles triangles often arise due to Theorem 10.2), properties of quadrilaterals, and circle properties covered in Class 9 (like relationships between chords and the center). The emphasis throughout remains on clear geometric reasoning, the accurate application of the relevant theorems, and, where necessary, the construction of structured, logical proofs.
Exercise 10.1
Question 1. How many tangents can a circle have?
Answer:
A circle is a collection of infinitely many points in a plane that are equidistant from a fixed point (the center).
A tangent to a circle is a line that intersects the circle at exactly one point, called the point of tangency.
For every point on the circumference of the circle, we can draw a unique tangent line passing through that point.
Since there are infinitely many points on the circumference of a circle, we can draw infinitely many tangent lines to the circle.
Therefore, a circle can have infinitely many tangents.
Question 2. Fill in the blanks
(i) A tangent to a circle intersects it in_____________point (s).
(ii) A line intersecting a circle in two points is called a ____________________.
(iii) A circle can have __________________parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called _______________
Answer:
(i) A tangent to a circle intersects it in one point (s).
(ii) A line intersecting a circle in two points is called a secant.
(iii) A circle can have two parallel tangents at the most.
(iv) The common point of a tangent to a circle and the circle is called point of contact.
Question 3. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is :
(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D) $\sqrt{119}$ cm.
Answer:
Given:
A circle with center O.
PQ is a tangent to the circle at point P.
Radius of the circle, OP = 5 cm.
Distance from the center O to point Q, OQ = 12 cm.
To Find:
The length of the tangent PQ.
Solution:
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, the radius OP is perpendicular to the tangent PQ at point P.
This means that $\triangle OPQ$ is a right-angled triangle with the right angle at P ($\angle OPQ = 90^\circ$).
In the right-angled triangle OPQ, OQ is the hypotenuse.
By the Pythagorean theorem:
$OP^2 + PQ^2 = OQ^2$
Substitute the given values:
$5^2 + PQ^2 = 12^2$
$25 + PQ^2 = 144$
Subtract 25 from both sides:
$PQ^2 = 144 - 25$
$PQ^2 = 119$
Take the square root of both sides:
$PQ = \sqrt{119}$
Since length must be positive, $PQ = \sqrt{119}$ cm.
Comparing this result with the given options:
The length PQ is $\sqrt{119}$ cm.
Therefore, option (D) is correct.
Question 4. Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Answer:
Here are the steps to draw the required figure:
1. Draw a circle with center O and any suitable radius.
2. Draw a line, let's call it line l, anywhere on the paper. This is the given line.
3. To draw the tangent parallel to line l:
- Draw a line perpendicular to line l passing through the center O of the circle. Let this perpendicular line intersect the circle at two points, say P and P'.
- Draw a line, let's call it line m, through point P (or P') such that line m is perpendicular to the line segment OP (or OP').
- Line m will be parallel to the given line l and will be tangent to the circle at point P (or P').
4. To draw the secant parallel to line l:
- Draw a line, let's call it line n, parallel to the given line l (and also parallel to the tangent line m).
- Ensure that this line n intersects the circle at two distinct points, say A and B.
- This can be achieved by drawing line n such that it lies between the tangent line m and the line passing through the center O parallel to l.
Following these steps, you will have a circle, a given line l, a tangent line m parallel to l, and a secant line n parallel to l.
Example 1 to 3 (Before Exercise 10.2)
Example 1. Prove that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
Answer:
Given:
Two concentric circles, $C_1$ (larger) and $C_2$ (smaller), with a common center O.
AB is a chord of the larger circle $C_1$ that is tangent to the smaller circle $C_2$ at point P.
To Prove:
The chord AB is bisected at the point of contact P, i.e., AP = PB.
Construction:
Join OP.
Proof:
Consider the smaller circle $C_2$.
AB is a tangent to the circle $C_2$ at the point P.
OP is the radius of the smaller circle $C_2$ through the point of contact P.
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
$OP \perp AB$
[Tangent is perpendicular to radius at point of contact]
Now, consider the larger circle $C_1$.
AB is a chord of the circle $C_1$.
OP is a line segment from the center O such that $OP \perp AB$.
We know that the perpendicular drawn from the center of a circle to a chord bisects the chord.
Therefore, OP bisects the chord AB.
This implies that P is the midpoint of AB.
Hence, AP = PB.
Thus, it is proved that in two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
Example 2. Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2 ∠OPQ.
Answer:
Given:
A circle with centre O.
An external point T.
TP and TQ are two tangents drawn from T to the circle at points P and Q respectively.
To Prove:
$\angle PTQ = 2 \angle OPQ$.
Proof:
We know that the lengths of tangents drawn from an external point to a circle are equal.
TP = TQ
(Tangents from external point T)
In triangle TPQ, since TP = TQ, it is an isosceles triangle.
Therefore, the angles opposite to equal sides are equal.
$\angle TPQ = \angle TQP$
(Angles opposite equal sides)
We also know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
OP $\perp$ TP
(Tangent is perpendicular to radius at point of contact)
So, $\angle OPT = 90^\circ$.
From the figure, we can write $\angle OPT$ as the sum of $\angle OPQ$ and $\angle TPQ$.
$\angle OPT = \angle OPQ + \angle TPQ$
$90^\circ = \angle OPQ + \angle TPQ$
Rearranging this equation to find $\angle TPQ$:
$\angle TPQ = 90^\circ - \angle OPQ$
...(i)
Now, consider the angle sum property of triangle TPQ:
$\angle PTQ + \angle TPQ + \angle TQP = 180^\circ$
Since $\angle TPQ = \angle TQP$, we can write:
$\angle PTQ + \angle TPQ + \angle TPQ = 180^\circ$
$\angle PTQ + 2 \angle TPQ = 180^\circ$
...(ii)
Substitute the expression for $\angle TPQ$ from equation (i) into equation (ii):
$\angle PTQ + 2 (90^\circ - \angle OPQ) = 180^\circ$
$\angle PTQ + 180^\circ - 2 \angle OPQ = 180^\circ$
Subtract $180^\circ$ from both sides:
$\angle PTQ - 2 \angle OPQ = 0$
$\angle PTQ = 2 \angle OPQ$
Hence Proved.
Example 3. PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (see Fig. 10.10). Find the length TP.
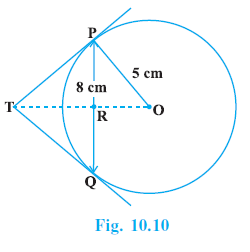
Answer:
Given:
A circle with centre O and radius OP = OQ = 5 cm.
PQ is a chord of length 8 cm.
Tangents at P and Q intersect at point T.
To Find:
The length of the tangent TP.
Construction:
Join OT. Let OT intersect the chord PQ at point R.
Solution:
We know that the line joining the centre of a circle to the external point from which tangents are drawn bisects the angle between the tangents and is the perpendicular bisector of the chord joining the points of contact.
Therefore, OT is the perpendicular bisector of PQ.
So, OR $\perp$ PQ and R is the midpoint of PQ.
PR = RQ = $\frac{PQ}{2} = \frac{8}{2} = 4$ cm.
Now, consider the right-angled triangle $\triangle ORP$ (right-angled at R).
By the Pythagorean theorem:
$OR^2 + PR^2 = OP^2$
Substitute the known values:
$OR^2 + 4^2 = 5^2$
$OR^2 + 16 = 25$
$OR^2 = 25 - 16 = 9$
$OR = \sqrt{9} = 3$ cm (Since length must be positive)
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
OP $\perp$ TP
[Tangent is perpendicular to radius at point of contact]
So, $\triangle OPT$ is a right-angled triangle with the right angle at P.
Let TP = $x$ and TR = $y$.
In right-angled $\triangle PRT$ (right-angled at R):
$TP^2 = PR^2 + TR^2$
$x^2 = 4^2 + y^2$
$x^2 = 16 + y^2$
...(i)
In right-angled $\triangle OPT$ (right-angled at P):
$OT^2 = OP^2 + TP^2$
From the figure, $OT = OR + TR = 3 + y$.
Substitute the values:
$(3 + y)^2 = 5^2 + x^2$
$9 + 6y + y^2 = 25 + x^2$
...(ii)
Substitute the value of $x^2$ from equation (i) into equation (ii):
$9 + 6y + y^2 = 25 + (16 + y^2)$
$9 + 6y + y^2 = 41 + y^2$
Subtract $y^2$ from both sides:
$9 + 6y = 41$
$6y = 41 - 9$
$6y = 32$
$y = \frac{32}{6} = \frac{16}{3}$ cm.
Now, substitute the value of $y$ back into equation (i) to find $x$ (which is TP):
$x^2 = 16 + y^2$
$x^2 = 16 + \left(\frac{16}{3}\right)^2$
$x^2 = 16 + \frac{256}{9}$
$x^2 = \frac{16 \times 9 + 256}{9}$
$x^2 = \frac{144 + 256}{9}$
$x^2 = \frac{400}{9}$
Take the square root:
$x = \sqrt{\frac{400}{9}} = \frac{20}{3}$
So, the length TP = $\frac{20}{3}$ cm.
Alternate Solution (Using Similar Triangles):
In $\triangle TRP$, $\angle TRP = 90^\circ$.
In $\triangle PRO$, $\angle PRO = 90^\circ$.
We know OP $\perp$ TP, so $\angle OPT = 90^\circ$.
$\angle OPR + \angle TPR = \angle OPT = 90^\circ$.
In right-angled $\triangle PRO$, $\angle POR + \angle OPR = 90^\circ$.
From these two equations, we have $\angle POR = \angle TPR$.
Now, consider $\triangle TRP$ and $\triangle PRO$.
$\angle TRP = \angle PRO = 90^\circ$
$\angle TPR = \angle POR$
(Proved above)
Therefore, by AA similarity criterion:
$\triangle TRP \sim \triangle PRO$
The corresponding sides are proportional:
$\frac{TR}{PR} = \frac{RP}{RO} = \frac{TP}{PO}$
We know PR = 4 cm, RO = 3 cm, and PO = 5 cm (radius).
Using the ratio $\frac{RP}{RO} = \frac{TP}{PO}$:
$\frac{4}{3} = \frac{TP}{5}$
Solving for TP:
$TP = \frac{4 \times 5}{3} = \frac{20}{3}$ cm.
Therefore, the length of TP is $\frac{20}{3}$ cm.
Exercise 10.2
In Q.1 to 3, choose the correct option and give justification.
Question 1. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
Answer:
Given:
Let the circle have center O.
Let Q be a point outside the circle.
Let P be the point of contact on the circle such that QP is the tangent.
Length of the tangent from Q to the circle, QP = 24 cm.
Distance of point Q from the center O, OQ = 25 cm.
To Find:
The radius of the circle, OP.
Solution:
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, the radius OP is perpendicular to the tangent QP at point P.
OP $\perp$ QP
This implies that $\triangle OPQ$ is a right-angled triangle with the right angle at P ($\angle OPQ = 90^\circ$).
In the right-angled triangle OPQ, the side opposite the right angle, OQ, is the hypotenuse.
By the Pythagorean theorem:
$OP^2 + QP^2 = OQ^2$
Let the radius OP be $r$. Substitute the given values:
$r^2 + 24^2 = 25^2$
$r^2 + 576 = 625$
Subtract 576 from both sides:
$r^2 = 625 - 576$
$r^2 = 49$
Take the square root of both sides:
$r = \sqrt{49}$
Since radius must be positive:
$r = 7$ cm
The radius of the circle is 7 cm.
Comparing this result with the given options:
Option (A) 7 cm is correct.
Question 2. In Fig. 10.11, if TP and TQ are the two tangents to a circle with centre O so that ∠ POQ = 110°, then ∠ PTQ is equal to
(A) 60°
(B) 70°
(C) 80°
(D) 90°
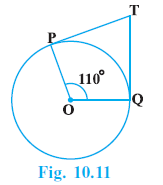
Answer:
Given:
A circle with centre O.
TP and TQ are tangents drawn from an external point T to the circle.
P and Q are the points of contact.
$\angle POQ = 110^\circ$.
To Find:
The measure of $\angle PTQ$.
Solution:
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Therefore, the radius OP is perpendicular to the tangent TP at point P, and the radius OQ is perpendicular to the tangent TQ at point Q.
$\angle OPT = 90^\circ$
[Tangent $\perp$ Radius]
$\angle OQT = 90^\circ$
[Tangent $\perp$ Radius]
Now, consider the quadrilateral OPTQ.
The sum of all interior angles of a quadrilateral is $360^\circ$.
Therefore, in quadrilateral OPTQ:
$\angle OPT + \angle POQ + \angle OQT + \angle PTQ = 360^\circ$
Substitute the known values into the equation:
$90^\circ + 110^\circ + 90^\circ + \angle PTQ = 360^\circ$
Add the known angles:
$290^\circ + \angle PTQ = 360^\circ$
Subtract $290^\circ$ from both sides to find $\angle PTQ$:
$\angle PTQ = 360^\circ - 290^\circ$
$\angle PTQ = 70^\circ$
Comparing this result with the given options:
The value of $\angle PTQ$ is $70^\circ$.
Therefore, option (B) 70° is correct.
Question 3. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to
(A) 50°
(B) 60°
(C) 70°
(D) 80°
Answer:
Given:
A circle with centre O.
PA and PB are tangents drawn from an external point P to the circle.
A and B are the points of contact.
The angle of inclination between the tangents, $\angle APB = 80^\circ$.
To Find:
The measure of $\angle POA$.
Solution:
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
OA $\perp$ PA
[Tangent $\perp$ Radius at point A]
OB $\perp$ PB
[Tangent $\perp$ Radius at point B]
So, $\angle OAP = 90^\circ$ and $\angle OBP = 90^\circ$.
Consider the triangles $\triangle OAP$ and $\triangle OBP$.
OA = OB
(Radii of the same circle)
PA = PB
(Lengths of tangents from an external point P are equal)
OP = OP
(Common side)
Therefore, by SSS congruence criterion:
$\triangle OAP \cong \triangle OBP$
By Corresponding Parts of Congruent Triangles (CPCT):
$\angle OPA = \angle OPB$
$\angle POA = \angle POB$
Since $\angle OPA = \angle OPB$, the line segment OP bisects the angle $\angle APB$.
$\angle OPA = \frac{1}{2} \angle APB$
Substitute the given value $\angle APB = 80^\circ$:
$\angle OPA = \frac{1}{2} \times 80^\circ = 40^\circ$
Now, consider the right-angled triangle $\triangle OAP$ (right-angled at A).
The sum of angles in a triangle is $180^\circ$.
$\angle POA + \angle OAP + \angle OPA = 180^\circ$
Substitute the known values $\angle OAP = 90^\circ$ and $\angle OPA = 40^\circ$:
$\angle POA + 90^\circ + 40^\circ = 180^\circ$
$\angle POA + 130^\circ = 180^\circ$
Subtract $130^\circ$ from both sides:
$\angle POA = 180^\circ - 130^\circ$
$\angle POA = 50^\circ$
Comparing this result with the given options:
The value of $\angle POA$ is $50^\circ$.
Therefore, option (A) 50° is correct.
Alternate Method (Using Quadrilateral Properties):
In quadrilateral OAPB:
$\angle OAP = 90^\circ$
$\angle OBP = 90^\circ$
$\angle APB = 80^\circ$ (Given)
Sum of angles in a quadrilateral = $360^\circ$.
$\angle AOB + \angle OAP + \angle APB + \angle OBP = 360^\circ$
$\angle AOB + 90^\circ + 80^\circ + 90^\circ = 360^\circ$
$\angle AOB + 260^\circ = 360^\circ$
$\angle AOB = 360^\circ - 260^\circ = 100^\circ$
Since $\triangle OAP \cong \triangle OBP$, we have $\angle POA = \angle POB$ (CPCT).
$\angle AOB = \angle POA + \angle POB = \angle POA + \angle POA = 2 \angle POA$
$2 \angle POA = 100^\circ$
$\angle POA = \frac{100^\circ}{2} = 50^\circ$
Option (A) 50° is correct.
Question 4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Answer:
Question 4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Answer:
Given:
A circle with centre O.
AB is a diameter of the circle.
Line $l$ is the tangent to the circle at point A.
Line $m$ is the tangent to the circle at point B.
To Prove:
The tangent lines $l$ and $m$ are parallel (i.e., $l \parallel m$).
Proof:
Since line $l$ is the tangent to the circle at point A, and OA is the radius through the point of contact A:
We know that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
OA $\perp$ line $l$
[Tangent $\perp$ Radius]
Therefore, $\angle OAl = 90^\circ$. Since AB is a straight line (diameter) passing through O, this implies:
$\angle BAl = 90^\circ$
... (i)
Similarly, since line $m$ is the tangent to the circle at point B, and OB is the radius through the point of contact B:
OB $\perp$ line $m$
[Tangent $\perp$ Radius]
Therefore, $\angle OBm = 90^\circ$. Since AB is a straight line (diameter) passing through O, this implies:
$\angle ABm = 90^\circ$
... (ii)
Now, consider the lines $l$ and $m$, and the diameter AB as a transversal line intersecting them.
From equations (i) and (ii), we have:
$\angle BAl = 90^\circ$
$\angle ABm = 90^\circ$
Thus, $\angle BAl = \angle ABm$.
These angles ($\angle BAl$ and $\angle ABm$) form a pair of alternate interior angles.
Since the alternate interior angles are equal, the lines $l$ and $m$ must be parallel.
$l \parallel m$
Hence, it is proved that the tangents drawn at the ends of a diameter of a circle are parallel.
Question 5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Answer:
Given:
A circle with centre O. AB is a tangent to the circle at the point of contact P. PQ is perpendicular to the tangent AB at P.
To Prove:
The perpendicular PQ passes through the centre O.
Proof:
We prove this by contradiction.
Let us assume that the perpendicular PQ at P does not pass through the centre O.
Since PQ is perpendicular to AB at P, we have:
$\angle\text{QPB} = 90^\circ$
... (i)
We know that the radius drawn to the point of contact is perpendicular to the tangent.
Therefore, OP is perpendicular to the tangent AB.
This means:
$\angle\text{OPB} = 90^\circ$
[Radius is perpendicular to the tangent at the point of contact] ... (ii)
From equations (i) and (ii), we have:
$\angle\text{QPB} = \angle\text{OPB}$
... (iii)
Equation (iii) implies that ray QP and ray OP are the same ray because they are both perpendicular to the same line AB at the same point P and lie on the same side of the line AB (assuming O and Q are on the same side of AB, which is typically how the diagram is drawn, or if on opposite sides, the contradiction still holds as they would form a straight line, but the angles being equal is the direct contradiction).
However, our initial assumption was that PQ does not pass through O, meaning Q and O are distinct points, which would make OP and QP distinct lines/rays.
The only way for $\angle\text{QPB}$ and $\angle\text{OPB}$ to be equal to $90^\circ$ and for Q and O to be distinct is if O lies on the extension of QP or vice versa, but that would mean both lines are perpendicular to AB at P, which is impossible unless they are the same line.
Thus, the equality $\angle\text{QPB} = \angle\text{OPB} = 90^\circ$ can only be true if the ray QP coincides with the ray OP.
This can happen only if Q lies on the ray OP or O lies on the ray QP. Since P is the point of contact and O is the center, the line OP is uniquely determined as the radius perpendicular to the tangent.
Therefore, the line PQ must pass through O.
This contradicts our assumption that PQ does not pass through O.
Hence, our assumption is false.
Therefore, the perpendicular at the point of contact to the tangent to a circle must pass through the centre.
Hence Proved.
Question 6. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Answer:
Given:
A circle with centre O.
Distance of point A from the centre O, OA = $5$ cm.
Length of the tangent from A to the circle, AP = $4$ cm (Let P be the point of contact).
To Find:
The radius of the circle (OP).
Solution:
We know that the radius drawn to the point of contact is perpendicular to the tangent.
Therefore, the radius OP is perpendicular to the tangent AP at the point of contact P.
This means that $\triangle$OPA is a right-angled triangle, with the right angle at P ($\angle\text{OPA} = 90^\circ$).
By the Pythagorean theorem in $\triangle$OPA, we have:
$OA^2 = OP^2 + AP^2$
[Pythagorean theorem]
Substitute the given values:
$(5)^2 = OP^2 + (4)^2$
$\$
$25 = OP^2 + 16$
$\$
Rearrange the equation to solve for $OP^2$:
$OP^2 = 25 - 16$
$\$
$OP^2 = 9$
$\$
Take the square root of both sides:
$OP = \sqrt{9}$
$\$
Since OP is a length, it must be positive.
$OP = 3$
$\$
The radius of the circle is $3$ cm.
Answer:
The radius of the circle is $3$ cm.
Question 7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Answer:
Given:
Two concentric circles with common centre O.
Radius of the larger circle, R = $5$ cm.
Radius of the smaller circle, r = $3$ cm.
Let AB be the chord of the larger circle that touches the smaller circle at point P.
To Find:
The length of the chord AB.
Solution:
Since AB is a tangent to the smaller circle at point P, the radius OP is perpendicular to the tangent AB at P.
Therefore, $\angle\text{OPA} = 90^\circ$.
In the larger circle, AB is a chord and OP is perpendicular to AB.
We know that the perpendicular drawn from the centre of a circle to a chord bisects the chord.
Therefore, P is the midpoint of AB, which means AP = PB.
Now consider the right-angled triangle $\triangle$OPA.
OA is the radius of the larger circle, so OA = R = $5$ cm.
OP is the radius of the smaller circle, so OP = r = $3$ cm.
AP is half the length of the chord AB.
By the Pythagorean theorem in $\triangle$OPA, we have:
$\text{OA}^2 = \text{OP}^2 + \text{AP}^2$
[Pythagorean theorem]
Substitute the known values:
$(5)^2 = (3)^2 + \text{AP}^2$
$\$
$25 = 9 + \text{AP}^2$
$\$
Subtract 9 from both sides:
$\text{AP}^2 = 25 - 9$
$\$
$\text{AP}^2 = 16$
$\$
Take the square root of both sides:
$\text{AP} = \sqrt{16}$
$\$
Since AP is a length, it must be positive.
$\text{AP} = 4$ cm
$\$
The length of the chord AB is twice the length of AP.
$\text{AB} = 2 \times \text{AP}$
$\$
$\text{AB} = 2 \times 4$
$\$
$\text{AB} = 8$ cm
$\$
Answer:
The length of the chord of the larger circle which touches the smaller circle is $8$ cm.
Question 8. A quadrilateral ABCD is drawn to circumscribe a circle (see Fig. 10.12). Prove that AB + CD = AD + BC
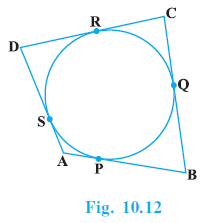
Answer:
Given:
A quadrilateral ABCD circumscribing a circle. The sides AB, BC, CD, and DA touch the circle at points P, Q, R, and S respectively.
To Prove:
AB + CD = AD + BC
Proof:
We know that the lengths of tangents drawn from an external point to a circle are equal.
Applying this property to the vertices A, B, C, and D, we get:
AP = AS
[Tangents from point A] ... (i)
BP = BQ
[Tangents from point B] ... (ii)
CR = CQ
[Tangents from point C] ... (iii)
DR = DS
[Tangents from point D] ... (iv)
Consider the left-hand side of the equation we need to prove: AB + CD.
We can write AB as the sum of AP and PB, and CD as the sum of CR and RD.
AB + CD = (AP + PB) + (CR + RD)
... (v)
Now, substitute the equal tangent lengths from equations (i), (ii), (iii), and (iv) into equation (v).
AB + CD = (AS + BQ) + (CQ + DS)
... (vi)
Rearrange the terms on the right-hand side of equation (vi).
AB + CD = AS + DS + BQ + CQ
... (vii)
Now, consider the right-hand side of the equation we need to prove: AD + BC.
We can write AD as the sum of AS and SD, and BC as the sum of BQ and QC.
AD + BC = (AS + DS) + (BQ + CQ)
... (viii)
Comparing equation (vii) and equation (viii), we see that the right-hand sides are identical.
Therefore, their left-hand sides must be equal.
AB + CD = AD + BC
[From (vii) and (viii)]
Thus, the sum of opposite sides of a quadrilateral circumscribing a circle are equal.
Hence Proved.
Question 9. In Fig. 10.13, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠ AOB = 90°.
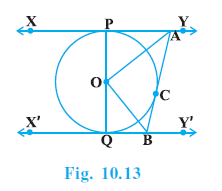
Answer:
Given:
A circle with centre O.
XY and X'Y' are two parallel tangents to the circle.
AB is another tangent at point C, which intersects XY at A and X'Y' at B.
To Prove:
$\angle\text{AOB} = 90^\circ$.
Construction:
Join OC. Let P and Q be the points of contact of the tangents XY and X'Y' respectively with the circle.
Proof:
Since XY and X'Y' are parallel tangents, the line segment PQ passing through the centre O is a diameter of the circle. Thus, POQ is a straight line.
Consider the tangents from point A to the circle, which are AP and AC. We know that the lengths of tangents drawn from an external point to a circle are equal.
So, AP = AC.
Also, OA is the common side, and OP = OC (radii of the same circle).
In $\triangle$OPA and $\triangle$OCA:
OP = OC
AP = AC
[Tangents from A]
OA = OA
$\triangle\text{OPA} \cong \triangle\text{OCA}$
[By SSS congruence rule]
By CPCT (Corresponding Parts of Congruent Triangles), we have:
$\angle\text{POA} = \angle\text{COA}$
... (i)
Similarly, consider the tangents from point B to the circle, which are BQ and BC.
So, BQ = BC.
Also, OB is the common side, and OQ = OC (radii of the same circle).
In $\triangle$OQB and $\triangle$OCB:
OQ = OC
BQ = BC
[Tangents from B]
OB = OB
$\triangle\text{OQB} \cong \triangle\text{OCB}$
[By SSS congruence rule]
By CPCT, we have:
$\angle\text{QOB} = \angle\text{COB}$
... (ii)
Since POQ is a straight line, the sum of the angles around O on this line is $180^\circ$.
$\angle\text{POA} + \angle\text{COA} + \angle\text{COB} + \angle\text{QOB} = 180^\circ$
[Angles on a straight line] ... (iii)
Substitute the equal angles from equations (i) and (ii) into equation (iii):
$\angle\text{COA} + \angle\text{COA} + \angle\text{COB} + \angle\text{COB} = 180^\circ$
$\$
$2\angle\text{COA} + 2\angle\text{COB} = 180^\circ$
$\$
Factor out 2:
$2(\angle\text{COA} + \angle\text{COB}) = 180^\circ$
$\$
Divide both sides by 2:
$\angle\text{COA} + \angle\text{COB} = \frac{180^\circ}{2}$
$\$
$\angle\text{COA} + \angle\text{COB} = 90^\circ$
... (iv)
From the figure, we can see that $\angle\text{AOB}$ is the sum of $\angle\text{COA}$ and $\angle\text{COB}$.
$\angle\text{AOB} = \angle\text{COA} + \angle\text{COB}$
... (v)
Substitute the result from equation (iv) into equation (v):
$\angle\text{AOB} = 90^\circ$
[From (iv) and (v)]
Hence Proved.
Question 10. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Answer:
Given:
A circle with centre O.
P is an external point from which two tangents PA and PB are drawn to the circle, touching the circle at points A and B respectively.
AB is the line-segment joining the points of contact.
To Prove:
The angle between the tangents ($\angle\text{APB}$) and the angle subtended by the line-segment joining the points of contact at the centre ($\angle\text{AOB}$) are supplementary.
That is, $\angle\text{APB} + \angle\text{AOB} = 180^\circ$.
Proof:
Consider the quadrilateral OAPB.
OA and OB are radii of the circle.
PA and PB are tangents to the circle at points A and B respectively.
We know that the radius drawn to the point of contact is perpendicular to the tangent.
Therefore, the angle between the radius OA and the tangent PA at point A is $90^\circ$. Similarly, the angle between the radius OB and the tangent PB at point B is $90^\circ$.
$\angle\text{OAP} = 90^\circ$
[Radius is perpendicular to tangent at contact point] ... (i)
$\angle\text{OBP} = 90^\circ$
[Radius is perpendicular to tangent at contact point] ... (ii)
The sum of the interior angles in any quadrilateral is $360^\circ$.
In quadrilateral OAPB, the sum of the angles is:
$\angle\text{AOB} + \angle\text{OBP} + \angle\text{BPA} + \angle\text{OAP} = 360^\circ$
[Sum of angles in a quadrilateral] ... (iii)
Substitute the values of $\angle\text{OAP}$ and $\angle\text{OBP}$ from equations (i) and (ii) into equation (iii):
$\angle\text{AOB} + 90^\circ + \angle\text{BPA} + 90^\circ = 360^\circ$
$\$
Combine the constant terms:
$\angle\text{AOB} + \angle\text{BPA} + 180^\circ = 360^\circ$
$\$
Subtract $180^\circ$ from both sides:
$\angle\text{AOB} + \angle\text{BPA} = 360^\circ - 180^\circ$
$\$
$\angle\text{AOB} + \angle\text{APB} = 180^\circ$
... (iv)
Equation (iv) shows that the sum of the angle subtended by the line-segment AB at the centre ($\angle\text{AOB}$) and the angle between the two tangents from P ($\angle\text{APB}$) is $180^\circ$.
Therefore, the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Hence Proved.
Question 11. Prove that the parallelogram circumscribing a circle is a rhombus.
Answer:
Given:
ABCD is a parallelogram circumscribing a circle. Let the circle touch the sides AB, BC, CD, and DA at points P, Q, R, and S respectively.
To Prove:
ABCD is a rhombus.
Proof:
Since ABCD is a parallelogram, we know that opposite sides are equal in length.
AB = CD
... (i)
BC = AD
... (ii)
We also know that the lengths of tangents drawn from an external point to a circle are equal.
Applying this property to the vertices of the parallelogram, which are external points to the circle, we have:
AP = AS
[Tangents from A] ... (iii)
BP = BQ
[Tangents from B] ... (iv)
CR = CQ
[Tangents from C] ... (v)
DR = DS
[Tangents from D] ... (vi)
Consider the sides of the parallelogram in terms of these tangent segments:
AB = AP + PB
... (vii)
BC = BQ + QC
... (viii)
CD = CR + RD
... (ix)
DA = DS + SA
... (x)
We know from property of tangents from an external point (as used in Question 8) that the sum of opposite sides of a quadrilateral circumscribing a circle are equal. So, AB + CD = BC + DA.
Substitute equations (i) and (ii) into this property:
AB + AB = BC + BC
[Using (i) and (ii)]
2AB = 2BC
$\$
Dividing both sides by 2, we get:
AB = BC
... (xi)
Now, combine equations (i), (ii), and (xi):
AB = CD
[From (i)]
BC = AD
[From (ii)]
AB = BC
[From (xi)]
Therefore, we have AB = BC = CD = AD.
A parallelogram in which all four sides are equal is a rhombus.
Thus, ABCD is a rhombus.
Hence Proved.
Question 12. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig. 10.14). Find the sides AB and AC.
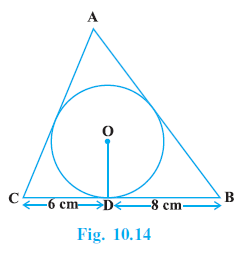
Answer:
Given:
A triangle ABC circumscribing a circle with centre O and radius r = $4$ cm.
The point of contact on BC is D, dividing BC into segments BD = $8$ cm and DC = $6$ cm.
To Find:
The lengths of sides AB and AC.
Solution:
Let the circle touch the sides AB at E and AC at F.
We know that the lengths of tangents drawn from an external point to a circle are equal.
From point B, the tangents are BD and BE.
BE = BD = $8$ cm
[Tangents from B]
From point C, the tangents are CD and CF.
CF = CD = $6$ cm
[Tangents from C]
From point A, the tangents are AE and AF.
Let AE = AF = $x$ cm.
The sides of the triangle are:
BC = BD + DC = $8 + 6 = 14$ cm
$\$
AB = AE + EB = $x + 8$ cm
$\$
AC = AF + FC = $x + 6$ cm
$\$
The radius of the inscribed circle is OD = OE = OF = $4$ cm.
We can find the area of $\triangle$ABC using two methods.
Method 1: Using Heron's Formula
Let a, b, c be the lengths of sides BC, AC, and AB respectively.
$a = 14$, $b = x+6$, $c = x+8$
$\$
The semi-perimeter s of $\triangle$ABC is:
$$s = \frac{a+b+c}{2} = \frac{14 + (x+6) + (x+8)}{2} = \frac{28 + 2x}{2} = 14+x$$
$\$
Now calculate $(s-a)$, $(s-b)$, and $(s-c)$:
$$s-a = (14+x) - 14 = x$$
$\$
$$s-b = (14+x) - (x+6) = 8$$
$\$
$$s-c = (14+x) - (x+8) = 6$$
$\$
Area of $\triangle$ABC using Heron's formula is:
$$\text{Area}(\triangle\text{ABC}) = \sqrt{s(s-a)(s-b)(s-c)}$$
$\$
$$\text{Area}(\triangle\text{ABC}) = \sqrt{(14+x)(x)(8)(6)} = \sqrt{48x(14+x)}$$
... (i)
Method 2: Using Sum of Areas of Triangles OAB, OBC, and OCA
Join OA, OB, and OC. The area of $\triangle$ABC is the sum of the areas of $\triangle$OBC, $\triangle$OCA, and $\triangle$OAB.
The radius from the centre to the point of contact is perpendicular to the tangent (side of the triangle). So, OD $\perp$ BC, OE $\perp$ AB, OF $\perp$ AC. The radius is the height of each smaller triangle with respect to the side as base.
$$\text{Area}(\triangle\text{OBC}) = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times \text{BC} \times \text{OD} = \frac{1}{2} \times 14 \times 4 = 28$$
$\$
$$\text{Area}(\triangle\text{OCA}) = \frac{1}{2} \times \text{AC} \times \text{OF} = \frac{1}{2} \times (x+6) \times 4 = 2(x+6)$$
$\$
$$\text{Area}(\triangle\text{OAB}) = \frac{1}{2} \times \text{AB} \times \text{OE} = \frac{1}{2} \times (x+8) \times 4 = 2(x+8)$$
$\$
Total Area of $\triangle$ABC:
$$\text{Area}(\triangle\text{ABC}) = \text{Area}(\triangle\text{OBC}) + \text{Area}(\triangle\text{OCA}) + \text{Area}(\triangle\text{OAB})$$
$\$
$$\text{Area}(\triangle\text{ABC}) = 28 + 2(x+6) + 2(x+8)$$
$\$
$$\text{Area}(\triangle\text{ABC}) = 28 + 2x + 12 + 2x + 16$$
$\$
$$\text{Area}(\triangle\text{ABC}) = 56 + 4x = 4(14+x)$$
... (ii)
Equating the two Area expressions
From equations (i) and (ii), we have:
$$\sqrt{48x(14+x)} = 4(14+x)$$
$\$
Square both sides:
$$48x(14+x) = (4(14+x))^2$$
$\$
$$48x(14+x) = 16(14+x)^2$$
$\$
Since $x$ represents a length, $x > 0$. Also, $14+x > 0$. We can divide both sides by $16(14+x)$.
$\$
$\$
Subtract x from both sides:
$\$
$\$
Divide by 2:
$\$
$\$
Now find the lengths of sides AB and AC using $x=7$:
AB = $x + 8 = 7 + 8 = 15$ cm
$\$
AC = $x + 6 = 7 + 6 = 13$ cm
$\$
Answer:
The length of side AB is $15$ cm and the length of side AC is $13$ cm.
Question 13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Answer:
Given:
A quadrilateral ABCD circumscribing a circle with centre O.
Let the sides AB, BC, CD, and DA touch the circle at points P, Q, R, and S respectively.
To Prove:
The angle subtended by opposite sides at the centre are supplementary. That is:
$\angle\text{AOB} + \angle\text{COD} = 180^\circ$
... (i)
And
$\angle\text{BOC} + \angle\text{DOA} = 180^\circ$
... (ii)
Construction:
Join OA, OB, OC, OD, OP, OQ, OR, and OS.
Proof:
Consider the triangles formed by the centre and the points where two tangents from a vertex touch the circle. For vertex A, consider $\triangle$OAP and $\triangle$OAS.
We know that the radius is perpendicular to the tangent at the point of contact.
$\angle\text{OAP} = 90^\circ$
[Radius $\perp$ Tangent]
$\angle\text{OAS} = 90^\circ$
[This statement is incorrect, OA is not perpendicular to AS or AP. Correct approach is using tangent properties.]
Let's use the property that the tangents from an external point to a circle are equally inclined to the line joining the point to the centre, and also the line joining the point to the centre bisects the angle subtended by the points of contact at the centre.
Alternatively, we can prove congruence of triangles directly:
In $\triangle$OAP and $\triangle$OAS:
OP = OS (Radii of the same circle)
AP = AS (Lengths of tangents from external point A)
OA = OA (Common side)
$\triangle\text{OAP} \cong \triangle\text{OAS}$
[By SSS congruence rule]
By CPCT (Corresponding Parts of Congruent Triangles), the angles subtended at the centre are equal:
$\angle\text{AOP} = \angle\text{AOS}$
... (iii)
Similarly, considering the other vertices:
$\angle\text{BOP} = \angle\text{BOQ}$
[Tangents from B] ... (iv)
$\angle\text{COR} = \angle\text{COQ}$
[Tangents from C] ... (v)
$\angle\text{DOR} = \angle\text{DOS}$
[Tangents from D] ... (vi)
The sum of all angles around the centre O is $360^\circ$.
$\angle\text{AOP} + \angle\text{AOS} + \angle\text{BOP} + \angle\text{BOQ} + \angle\text{COR} + \angle\text{COQ} + \angle\text{DOR} + \angle\text{DOS} = 360^\circ$
... (vii)
Using equations (iii) to (vi), substitute the equal angles into equation (vii):
$\angle\text{AOS} + \angle\text{AOS} + \angle\text{BOQ} + \angle\text{BOQ} + \angle\text{COQ} + \angle\text{COQ} + \angle\text{DOS} + \angle\text{DOS} = 360^\circ$
$\$
$2\angle\text{AOS} + 2\angle\text{BOQ} + 2\angle\text{COQ} + 2\angle\text{DOS} = 360^\circ$
$\$
Divide by 2:
$\angle\text{AOS} + \angle\text{BOQ} + \angle\text{COQ} + \angle\text{DOS} = 180^\circ$
... (viii)
Now, consider the angle subtended by side AB at the centre, which is $\angle\text{AOB}$.
$\angle\text{AOB} = \angle\text{AOP} + \angle\text{BOP}$
... (ix)
Using equations (iii) and (iv), we can write this as:
$\angle\text{AOB} = \angle\text{AOS} + \angle\text{BOQ}$
... (x)
Consider the angle subtended by the opposite side CD at the centre, which is $\angle\text{COD}$.
$\angle\text{COD} = \angle\text{COR} + \angle\text{DOR}$
... (xi)
Using equations (v) and (vi), we can write this as:
$\angle\text{COD} = \angle\text{COQ} + \angle\text{DOS}$
... (xii)
Add equation (x) and equation (xii):
$\angle\text{AOB} + \angle\text{COD} = (\angle\text{AOS} + \angle\text{BOQ}) + (\angle\text{COQ} + \angle\text{DOS})$
$\$
Rearrange the terms on the right side:
$\angle\text{AOB} + \angle\text{COD} = \angle\text{AOS} + \angle\text{BOQ} + \angle\text{COQ} + \angle\text{DOS}$
$\$
From equation (viii), we know that $\angle\text{AOS} + \angle\text{BOQ} + \angle\text{COQ} + \angle\text{DOS} = 180^\circ$.
Therefore,
$\angle\text{AOB} + \angle\text{COD} = 180^\circ$
[From (viii)]
This proves the first part.
Now, consider the angle subtended by side BC at the centre, which is $\angle\text{BOC}$.
$\angle\text{BOC} = \angle\text{BOQ} + \angle\text{COQ}$
... (xiii)
Consider the angle subtended by the opposite side DA (or AD) at the centre, which is $\angle\text{DOA}$.
$\angle\text{DOA} = \angle\text{DOS} + \angle\text{AOS}$
... (xiv)
Add equation (xiii) and equation (xiv):
$\angle\text{BOC} + \angle\text{DOA} = (\angle\text{BOQ} + \angle\text{COQ}) + (\angle\text{DOS} + \angle\text{AOS})$
$\$
Rearrange the terms on the right side:
$\angle\text{BOC} + \angle\text{DOA} = \angle\text{AOS} + \angle\text{BOQ} + \angle\text{COQ} + \angle\text{DOS}$
$\$
Again, from equation (viii), we know that $\angle\text{AOS} + \angle\text{BOQ} + \angle\text{COQ} + \angle\text{DOS} = 180^\circ$.
Therefore,
$\angle\text{BOC} + \angle\text{DOA} = 180^\circ$
[From (viii)]
This proves the second part.
Thus, the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Hence Proved.